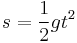Two New Sciences

The Discourses and Mathematical Demonstrations Relating to Two New Sciences (Discorsi e dimostrazioni matematiche, intorno à due nuove scienze, 1638) was Galileo's final book and a sort of scientific testament covering much of his work in physics over the preceding thirty years.

After his Dialogue Concerning the Two Chief World Systems, the Roman Inquisition had banned publication of any work by Galileo, including any he might write in the future.^[1] After the failure of attempts to publish the work in France, Germany, or Poland, it was picked up by Lodewijk Elzevir in Leiden, The Netherlands, where the writ of the Inquisition was of little account (see House of Elzevir).

The same three men as in the Dialogue carry on the discussion, but they have changed. Simplicio, in particular, is no longer the stubborn and rather dense Aristotelian; to some extent he represents the thinking of Galileo's early years, as Sagredo represents his middle period. Salviati remains the spokesman for Galileo.

Contents 1 The Science of materials 2 The Law of falling bodies 3 Infinity 4 Reactions by Commentators 4.1 The flow of time 5 Notes 6 References 7 External links

The Science of materials

The sciences named in the title are the strength of materials and the motion of objects. Galileo worked on an additional section on the force of percussion, but was not able to complete it to his own satisfaction.

The discussion begins with a demonstration of the reasons that a large structure proportioned in exactly the same way as a smaller one must necessarily be weaker known as the square-cube law. Later in the discussion this principle is applied to the thickness required of the bones of a large animal, possibly the first quantitative result in biology, anticipating J.B.S. Haldane's seminal work On Being the Right Size, and other essays, edited by John Maynard Smith.

The Law of falling bodies

Thomas Bradwardine was the first to formulate the equation for the displacement s of a falling object, which starts from rest, under the influence of gravity for a time t (the essential principle had been previously stated by the Oxford Calculators):

In Two New Sciences Galileo (Salviati speaks for him) used a wood molding, "12 cubits long, half a cubit wide and three finger-breadths thick" as a ramp with a straight, smooth, polished groove to study rolling balls ("a hard, smooth and very round bronze ball"). He lined the groove with "parchment, also smooth and polished as possible". He inclined the ramp at various angles, effectively slowing down the acceleration enough so that he could measure the elapsed time. He would let the ball roll a known distance down the ramp, and used a water clock to measure the time taken to move the known distance; this clock was

"a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results."^[2]

Infinity

The book also contains a discussion of infinity. Galileo considers the example of numbers, and their squares. He starts by noting that it cannot be denied that there are as many as there are numbers because every number is a root of some square:

1 <--> 1, 2 <--> 4, 3 <--> 9, 4 <--> 16, and so on.

(In modern terms, it is possible to have a one-to-one correspondence between the elements of a set N and the elements of a proper subset S of N). But he notes what appears to be a contradiction: Yet at the outset we said there are many more numbers than squares, since the larger portion of them are not squares. Not only so, but the proportionate number of squares diminishes as we pass to larger numbers.

He resolves the contradiction by denying the possibility of comparing infinite numbers: we can only infer that the totality of all numbers is infinite, that the number of squares is infinite, and that the number of their roots is infinite; neither is the number of squares less than the totality of all numbers, nor the latter greater than the former; and finally the attributes "equal," greater," and "less," are not applicable to infinite, but only to finite, quantities. Indeed, he denies that an infinite quantity can meaningfully be said to be greater than a finite quantity. This is a possible resolution, and it implicitly recognises that he has no definition of comparison for infinite numbers, but is less powerful than the modern resolution.

How does this arise in the dialogues? Galileo is discussing problems arising from rolling circles: if two concentric circles of different radius roll along lines, then if the larger does not slip, it appears clear that the smaller must slip. But in what way? Galileo attempts to clarify the matter by considering hexagons, and then extending to rolling polygons with 100,000 sides, or any arbitrarily large number, where he shows that a finite number of finite slips occur on the inner shape. Eventually he concludes that The line traversed by the larger circle consists then of an infinite number of points which completely fill it; while that which is traced by the smaller circle consists of an infinite number of points which leave empty spaces and only partly fill the line, which would not be considered satisfactory now.

Reactions by Commentators

"So great a contribution to physics was Two New Sciences that scholars have long maintained that the book anticipated Isaac Newton's laws of motion."^[3]

"Galileo ... is the father of modern physics—indeed of modern science"—Albert Einstein.^[4]

The flow of time

• The water clock mechanism described above was engineered to provide laminar flow of the water during the experiments, thus providing a constant flow of water for the durations of the experiments, and embodying what Newton called duration. In particular, Galileo ensured that the vat of water was large enough to provide a uniform jet of water.
• Galileo's experimental setup to measure the literal flow of time (see above), in order to describe the motion of a ball, was palpable enough and persuasive enough to found the sciences of mechanics and kinematics. Time in physics, in particular, could be founded on the notion of the linear flow of time.

• The law of falling bodies was discovered in 1599. But in the 20th century some authorities challenged the reality of Galileo's experiments, in particular the French historian of science Alexandre Koyré. The experiments reported in Two New Sciences to determine the law of acceleration of falling bodies, for instance, required accurate measurements of time, which appeared to be impossible with the technology of 1600. According to Koyré, the law was arrived at deductively, and the experiments were merely illustrative thought experiments.
  • Later research, however, has validated the experiments. The experiments on falling bodies (actually rolling balls) were replicated using the methods described by Galileo (Settle, 1961), and the precision of the results was consistent with Galileo's report. Later research into Galileo's unpublished working papers from as early as 1604 clearly showed the reality of the experiments and even indicated the particular results that led to the time-squared law (Drake, 1973).^[5]

Notes

1. ^ (Drake 1978, p. 367). See Galileo affair for further details.
2. ^ Galileo 1638 Discorsi e dimostrazioni matematiche, intorno à due nuove scienze 213, Leida, Appresso gli Elsevirii (Leiden: Louis Elsevier), or Mathematical discourses and demonstrations, relating to Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914. Section 213 is reprinted on pages 534-535 of On the Shoulders of Giants: The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
3. ^ Stephen Hawking, ed. p. 397, On the Shoulders of Giants.
4. ^ Stephen Hawking, ed. p. 398, On the Shoulders of Giants.
5. ^ Stillman Drake (1973). "Galileo's Discovery of the Law of Free Fall". Scientific American v. 228, #5, pp. 84-92.

References

• Drake, Stillman, translator (1974). Two New Sciences, University of Wisconsin Press, 1974. ISBN 0-299-06404-2. A new translation including sections on centers of gravity and the force of percussion.

• Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5. 

• Henry Crew and Alfonso de Salvio, translators, [1914] (1954). Dialogues Concerning Two New Sciences, Dover Publications Inc., New York, NY. ISBN 486-60099-8. The classic source in English, originally published by McMillan (1914).

• Titles of the first editions taken from Leonard C. Bruno 1989, The Landmarks of Science: from the Collections of the Library of Congress. ISBN 0-8160-2137-6 Q125.B87

External links

• (Italian) Italian text with figures
• English translation by Crew and de Salvio, with original figures
• Another on-line copy of Crew and de Salvio's translation
• Galileo Galilei: The Falling Bodies Experiment - Background and experiments.